适用问题:
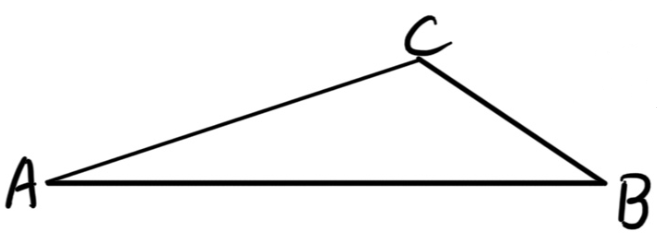
在 △ACB 中,∠ACB=α,AB=a(α,a 均为定值),求 mAC+nBC 的最大值。
结论: (mAC+nBC)max=sinαn2+2mncosα+m2⋅a。
推导过程: 将原式转化为 m(AC+mnBC)。
- 当 α>90∘ 时:
(i) mn>−cosα
延长 AC 至 D,使得 CD=mnBC,作 BH⊥AD,如图:
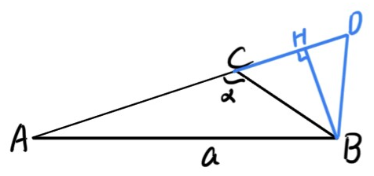
令 λ=mn, CH=BC⋅(−cosα), DH=CD−CH=(λ+cosα)BC。
BH=BC⋅sinα。
∴tan∠ADB=DHHB=λ+cosαsinα, (⇔∠ADB=arctanλ+cosαsinα)。
可以求出 sin∠ADB=λ2+2λcosα+1sinα。
∠ADB 为定角,AB 为定弦 ⇒ D 在 △ADB 的外接圆上运动。
则 △ADB 的外接圆半径的 2 倍 2r=sin∠ADBAB=sinαa⋅λ2+2λcosα+1。
∵AD≤2r
∴ADmax=sinαλ2+2λcosα+1⋅a。
(ii) mn<−cosα
延长 AC 至 D,使得 CD=mnBC,作 BH⊥AD,如图:
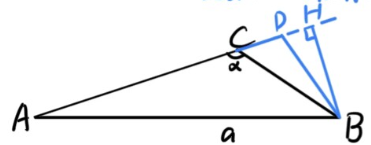
令 λ=mn,CH=BC⋅(−cosα), DH=CH−CD=(−λ−cosα)BC。
BH=BC⋅sinα。
∴tan∠HDB=DHHB=−λ+cosαsinα。
∴tan∠ADB=−tan∠DHB=λ+cosαsinα (⇔∠ADB=arctanλ+cosαsinα)
∠ADB 为定角,AB 为定弦 ⇒ D 在 △ADB 的外接圆上运动。
可以求出 sin∠ADB=λ2+2λcosα+1sinα。
则 △ADB 的外接圆半径的 2 倍 2r=sin∠ADBAB=sinαa⋅λ2+2λcosα+1。
∵AD≤2r
∴ADmax=sinαλ2+2λcosα+1⋅a。
- 当 α<90∘ 时:
延长 AC 至 D,使得 CD=mnBC,作 BH⊥AD,如图:
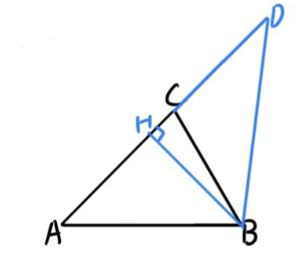
令 λ=mn。
CH=BC⋅cosα,DH=CD+CH=(λ+cosα)BC。
BH=BC⋅sinα。
∴tan∠ADB=DHHB=λ+cosαsinα, (⇔∠ADB=arctanλ+cosαsinα)。
∠ADB 为定角,AB 为定弦 ⇒ D 在 △ADB 的外接圆上运动。
可以求出 sin∠ADB=λ2+2λcosα+1sinα。
则 △ADB 的外接圆半径的 2 倍 2r=sin∠ADBAB=sinαa⋅λ2+2λcosα+1。
∵AD≤2r
∴ADmax=sinαλ2+2λcosα+1⋅a。
综上,(AC+mn⋅BC)max=ADmax=sinαλ2+2λcosα+1⋅a。
⇔(m⋅AC+n⋅BC)max=m⋅ADmax=sinαm2+2mncosα+n2⋅a。



